Artikel Image Recognition [Ir]
Image Recognition bzw. die Bilderkennung ist eines der zwölf „Assess“-Elemente des Periodensystems der KI. Dabei geht es darum, Bilder bzw. einzelne Objekte innerhalb der Bilder zu klassifizieren. Was als „Bild“ verstanden wird, kann vielfältig sein. Verbreitet ist es beispielsweise RGB-Bilder, Infrarotbilder oder Röntgenaufnahmen als Input zu verwenden. Allerdings kann die Anwendung über das Bildverständnis eines Menschen hinaus gehen.
https://www.periodensystem-ki.de/KI-Elemente/Ir
Ebenso vielseitig können die praktischen Anwendungsfälle sein. Zu nennen ist hierbei zum Beispiel das autonome Fahren, wobei durch Bilderkennung andere Fahrzeuge oder Fußgänger erkannt werden (Feng et al., 2021). Genauso kann die Bilderkennung aber auch in der Medizin eingesetzt werden, um beispielsweise Tumore in Ultraschallbildern zu erkennen (Cao et al. 2017).
Convolutional Neural Networks
Als großer Durchbruch der modernen Bilderkennung gilt das AlexNet (Krizhevsky et al 2012). Beim ILSVRC-2012 Bilderkennungswettbewerb konnte mit AlexNet eine Top-5 Testfehlerrate von 15,3 % erreicht werden. Dieses Ergebnis sorgte für Aufsehen, da die Fehlerrate nahezu halb so hoch war, wie die Fehlerrate der nächstbesten Einsendung, welche 26,2 % erreicht hatte.
AlexNet setzt dabei auf ein sogenanntes Convolutional Neural Network (CNN) – ein Ansatz, welcher zwar schon durch erste Pionierarbeiten, wie das Neocognitron (Fukushima et al. 1980) und LeNet (LeCun et al. 1990) bekannt war, sich aufgrund mangelnder Computerleistung zur damaligen Zeit nicht durchsetzen konnte. Seit AlexNet arbeiten die meisten modernen Bilderkennungsmethoden mit diesem Ansatz.
Das Convolutional Neural Network ist eine besondere Art neuronaler Netze, welche sich speziell zur Bilderkennung eignet. Die zentralen Grundbausteine des Netzwerks sind dabei Convolution Layers, Subsampling- bzw. Pooling Layers und Fully Connected Layers, welche zwischen einem Input- und einem Output Layer eingespannt sind. (Wang et al. 2019)
Input
Als Input dient in der Regel ein digitales Bild. Dabei wird jeder Farbkanal durch eine Matrix repräsentiert. Dementsprechend werden bei einem RGB-Bild drei Matrizen verwendet, während bei verschiedenen Formen von Schwarzweißbildern, wie zum Beispiel Infrarotbildern oder Röntgenbildern, eine Matrix genügt. Zur Verbesserung der Verständlichkeit gehen wir von nun an von einem Schwarzweiß-Input aus. Jedes Element der Matrix steht für ein Pixel des Bildes. Die Elemente sind dabei in der Regel numerische Werte zwischen 0 und 255 oder zwischen 0 und 1.
Die Grafik zeigt eine Überlagerung der optischen Darstellung mit hellen und dunklen Pixeln und der Darstellung mit numerischen Werten.
Convolution Layers
Das englische Wort Convolution bedeutet so viel wie Faltung. Mit Hilfe der Faltungen werden sogenannte Featuremaps erzeugt, welche dazu dienen, je nach Art der Faltung, verschiedene Merkmale des Bildes zu extrahieren. Zur Erzeugung der Faltungen werden Kernels verwendet. Dabei handelt es sich um Matrizen einer vordefinierten Größe (Kernel-Size) mit trainierbaren Gewichten. Die Gewichte des Kernels bilden mit den Pixel-Werten des Bildes ein Skalarprodukt, um die einzelnen Werte der resultierenden Featuremap zu bestimmen. Dieser Kernel wandert mit einer zuvor definierten Schrittlänge (Stride-Length) über den gesamten Input. In der Regel werden mehrere Kernels mit unterschiedlichen Gewichten gleichzeitig verwendet, wodurch verschiedene Featuremaps entstehen. (Wang et al. 2019)
Um die Featuremap zu finalisieren, wird noch ein Bias und eine Aktivierungsfunktion benötigt.
Als Bias versteht man einen trainierbaren Zahlenwert, der positiv oder auch negativ sein kann, welcher zu allen Werten der jeweiligen Featuremap dazu addiert wird. Die Aktivierungsfunktion ist eine mathematische Funktion, die auf sämtliche Werte angewendet wird, welche das Neuron ausgibt. Bei CNNs wird in der Regel die ReLU-Aktivierungsfunktion verwendet. Diese gibt für alle Werte, welche kleiner als Null sind, Null zurück, ansonsten ist der Eingabewert auch der Ausgabewert. (Wang et al. 2019)
Die folgende Grafik stellt diesen Vorgang visuell dar:
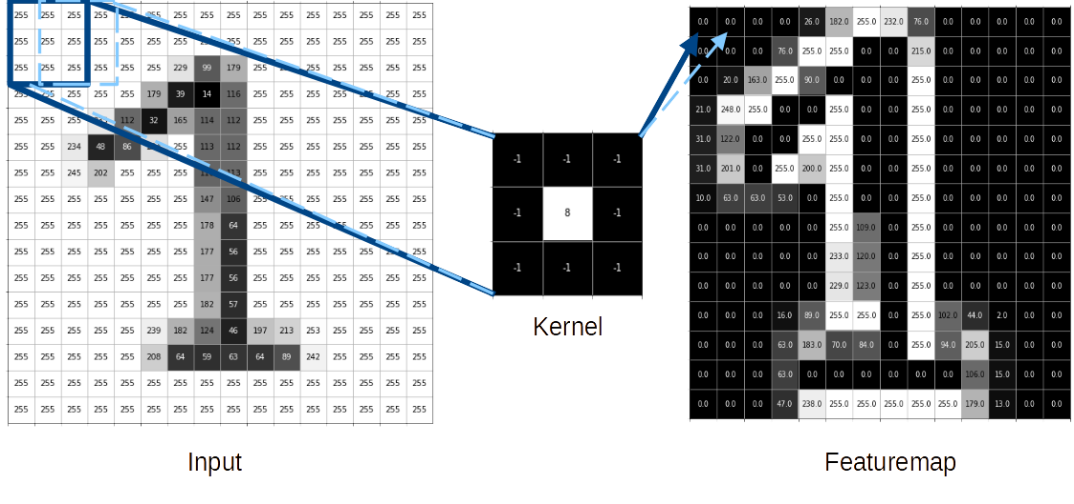
Hier wird das Bild der eins von einem 3×3 Kernel mit einer Stride-Length von einem Pixel abgetastet. Der Bias ist in diesem Fall null. Um den Effekt des Kernels besser sehen zu können, wird nicht die normale ReLU-Aktivierungsfunktion verwendet, sondern diese wird um einen zusätzlichen Cutoff bei 255 erweitert. (In einem „echten“ CNN sollte aber in aller Regel hier die ReLU-Aktivierungsfunktion verwendet werden.) Anhand der resultierenden Featuremap ist zu erkennen, dass die Gewichte des Kernels alle Kanten des Bildes hervorheben.
Pooling Layers
Die Pooling Layers, welche teilweise auch Subsampling Layers genannt werden, wechseln sich in der Regel periodisch mit den Convolution Layers ab. Sie dienen dazu, die Größe der eingegebenen Featuremap zu verringern und somit die Komplexität des Netzwerks und die Anzahl der Parameter zu reduzieren. Häufig wird dazu das Max-Pooling verwendet. Dabei wandert, ähnlich wie bei den Convolution Layers, auch ein Kernel (mit einer bestimmten Kernel-Size und einer bestimmten Stride-Length) über die gegebene Featuremap. Allerdings enthält dieser Kernel keine trainierbaren Gewichte. Stattdessen übernimmt der Pooling Kernel jeweils den höchsten Wert innerhalb des Pooling-Kernels in die erzeugte Pooled Feature Map. (Wang et al. 2019)
Dieser Prozess kann folgendermaßen aussehen:
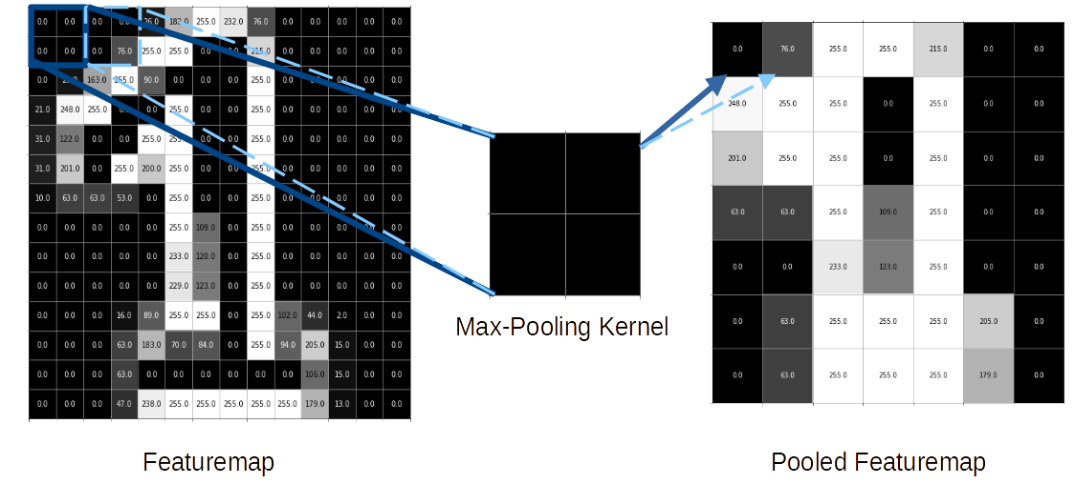
In diesem Beispiel wird ein Max-Pooling Kernel mit der Größe 2×2 verwendet, welcher sich mit einer Stride-Length von zwei Pixeln über die Featuremap bewegt. Dadurch wird die Featuremap der Größe 14×14 zu einer Pooled Featuremap der Größe 7×7 komprimiert.
Fully Connected Layer
Zum Schluss muss auf Basis der erstellten Featuremaps noch eine Klassifizierung durchgeführt werden. Hierzu werden die Featuremaps zunächst in Vektoren umgewandelt. Sogenannte Fully Connected Layers dienen anschließend dazu, aus den Vektoren die einzelnen Klassenwahrscheinlichkeiten zu ermitteln. Dabei sind sämtliche Neuronen einer Schicht mit sämtlichen Neuronen der darauffolgenden Schicht verbunden. Diese Fully Connected Layers führen zu einem Output-Layer, bei dem die Anzahl an Neuronen der Anzahl der möglichen Klassen entspricht. Die Softmax-Funktion dient beim Output als Aktivierung, da diese eine Normalisierung beinhaltet, wodurch alle Werte des ausgegebenen Vektors in der Summe 1 ergeben. (Wang et al. 2019)
Das gesamte Netzwerk
Fügt man nun alle beschriebenen Schichten zusammen, erhält man ein Convolutional Neural Network. Die nachfolgende Abbildung zeigt beispielhaft das LeNet.
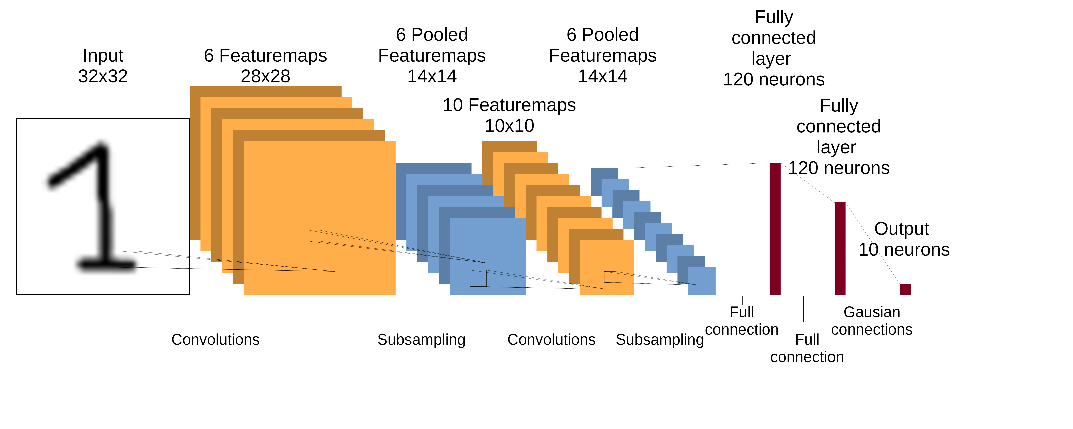
Quellen
https://periodensystem-ki.de/KI-Elemente/Ir , aufgerufen am 19.05.2023
Feng, D., Harakeh, A., Waslander, S.L. and Dietmayer, K., 2021. A review and comparative study on probabilistic object detection in autonomous driving. IEEE Transactions on Intelligent Transportation Systems, 23(8), pp.9961-9980
Cao, Z., Duan, L., Yang, G., Yue, T., Chen, Q., Fu, H. and Xu, Y., 2017. Breast tumor detection in ultrasound images using deep learning. In Patch-Based Techniques in Medical Imaging: Third International Workshop, Patch-MI 2017, Held in Conjunction with MICCAI 2017, Quebec City, QC, Canada, September 14, 2017, Proceedings 3 (pp. 121-128). Springer International Publishing.
Krizhevsky A., Sutskever I., Hinton G.E, 2012. Imagenet classification
with deep convolutional neural networks. In NIPS.
Fukushima K., 1980.Neocognitron: A self-organizing neural network model
for a mechanism of pattern recognition unaffected by shift in position,
Biological cybernetics.
LeCun Y., Bottou L., Bengio Y.,Haffner P., 1998. Gradient-based
learning applied to document recognition, Proceedings of the IEEE,
Wang, W., Yang, Y., Wang, X., Wang, W. and Li, J., 2019. Development of convolutional neural network and its application in image classification: a survey. Optical Engineering, 58(4), pp.040901-040901
Rechtliches
Hochschule für Technik, Wirtschaft und Medien Offenburg
| Campus Offenburg
Badstraße 24 77652 Offenburg Tel (+49) 781 205-0 Fax (+49) 781 205-214 |
Campus Gengenbach
Klosterstraße 14 77723 Gengenbach Tel (+49) 7803 9698-0 Fax (+49) 7803 9698-4449 |